数学という学問にはみなさん馴染みがあると思いますが、応用数学とはどのような学問なのでしょうか？応用数学を定義するなら、「数学の理論や手法を他分野へ応用できる形に整備したり、実際に他分野へ応用したりする学問領域」といったところになるでしょうか。
歴史を見ると、数学と他分野の結びつきに関する「自然という書物は数学の言葉で書かれている」というガリレオの有名なことばがあります。分かりやすいことばでいいかえれば、自然の法則や規則は数学の式で書くことができる、といってよいでしょう。実際、ガリレオは落下する物体の法則などを、数学を使って記述しました。さらに、応用数学の発展にはニュートン力学が大いに関係しています。微積分、微分方程式などの新しい分野がニュートン力学へ応用するために整備されました。つまり、既存の「数学の言葉」では足りず、微積分、微分方程式などの新しい「数学の言葉」を作って自然法則を記述したことになります。このころの応用数学とニュートン力学の関係は非常に密接で、19世紀中頃まで応用数学者とニュートン力学の研究者の間に明確な区別はありませんでした。このようなことから、上の定義でいえば最初の「他分野」は力学であったといえるでしょう。
その後、「他分野」は電磁気学、流体力学、量子力学、相対性理論など物理学のその他の分野、さらには物理学以外の分野にも及び、現在の応用数学は非常に多くの分野と関連を持っています。物理学、化学、生物学などの理学の伝統的な分野のほか、コンピュータサイエンス、データサイエンスやAIなどの新しい分野、また、制御、機械、通信などの工学のいろいろな分野、さらに、経済学を始めとする社会科学など文系の分野も「他分野」に入ります。
非常に多くの「他分野」が登場しますが、幸いなことに、分野が異なっても同じ「数学の言葉」、つまり、同じ数学の理論や手法が利用できることはよくあります。一番利用できるのは微積分と線形代数でしょう。そこで本学科では、まず、1年生で微積分と線形代数、コンピュータを利用するときに必要となるプログラミングを学びます。その後、データサイエンスを支える統計学、シミュレーションなどで活躍する数値計算とそのアルゴリズム、コンピュータに知的な処理を行わせる際に基礎となる離散数学やコンピュータサイエンスなどを学習します。このようにして幅広い「他分野」に対応できる応用数学の力をつけてもらうことが本学科の教育の目標です。
実社会で取り扱われている「データ」の分析手法を探求する学問領域です。複雑な現象を統計的に予測・解明するために、様々な統計手法の数理的内容を深く学び、数学的に解く理論と方法論を学習します。
自然科学、社会科学等における複雑な現象の本質を理解・予測するための数学的なモデル化やコンピュータシミュレーションに関する学問領域です。定式化や解析、計算アルゴリズムの設計・開発等、基礎理論から応用・実践まで総合的に学習します。
応用数学科では、数理データサイエンス・数理モデリング・知能数理の３分野の基礎から専門的な内容までを一貫して学習するために以下のようなカリキュラムを編成しています。４年次で行う卒業研究では３年次までの科目に比べ、より能動的な学習姿勢が求められます。
応用数学科では、中学校教諭一種（数学）と高等学校教諭一種（数学・情報）の教員免許状が取得できます。また、大学院（応用数学専攻）では、中学校教諭専修（数学）と高等学校教諭専修（数学）の教員免許状が取得できます。教員免許状を取得するためには、卒業するために必要な単位に加え、教職課程科目の単位の取得が必要となります。教職課程科目についてはこちらをご覧ください。
なお、応用数学科を含め東京理科大学では、教職課程の履修が１年次より始まります。教職課程を履修するには、教職課程登録が必要です。教職課程についての詳細はこちらをご覧ください。
現代社会は多種多様なデータで溢れかえっています。そのデータから価値ある情報を見出し、データに基づいて合理的な判断を行うことを可能とするデータサイエンティストが社会では求められています。本学では、データサイエンスに関する基礎知識や応用力を身につけるため、データサイエンス教育プログラムが導入されています。データサイエンス教育プログラムは、学部生対象の「基礎」、そして大学院生対象の「専門」の２種から構成されています。
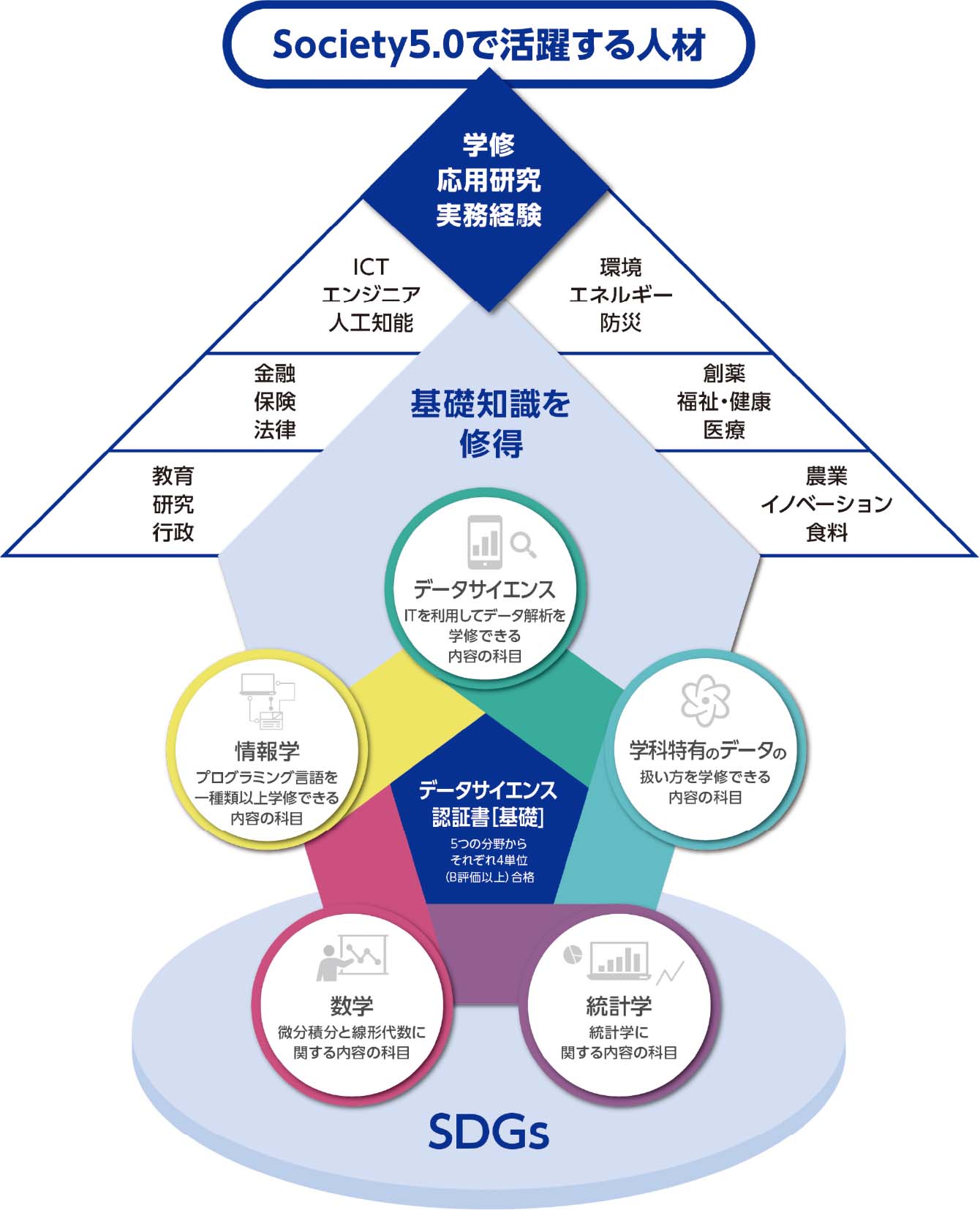
データサイエンスに関する基礎知識やリテラシーを学修する教育プログラムです。本プログラムに関する科目の単位取得により、修了要件を満たした場合には、本学オリジナルの「データサイエンス認証書[基礎](Data Science Certificate [Basic])」を授与します。
サイバー空間（仮想空間）とフィジカル空間（現実空間）を高度に融合させたシステムにより、経済発展と社会的課題の解決を両立する、人間中心の社会（Society）のことです。狩猟社会（Society 1.0）、農耕社会（Society 2.0）、工業社会（Society 3.0）、情報社会（Society 4.0）に続く、新たな社会を指すもので、第５期科学技術基本計画において我が国が目指すべき未来社会の姿として初めて提唱されました。（「内閣府」より）
持続可能な開発目標（SDGs：Sustainable Development Goals）とは、2001年に策定されたミレニアム開発目標（MDGs）の後継として、2015年9月の国連サミットで加盟国の全会一致で採択された「持続可能な開発のための2030アジェンダ」に記載された、2030年までに持続可能でよりよい世界を目指す国際目標です。（「外務省」より）
５つの各分野[①数学、②統計学、③情報学、④データサイエンス、⑤その他(学科特有のデータを扱う授業)]からそれぞれ４単位をB評価以上の成績で合格(合計20単位)すること。
応用数学科の学生は、他学科開講の講義を履修しなくても、卒業に必要な応用数学科独自の科目のみで、修了要件を満たせば認定証を取得できます。
| 分 野 | 定 義 |
|---|---|
| ①数 学 | 微分積分と線形代数に関する内容を含む科目を配置する分野 |
| ②統計学 | 統計学に関する内容を含む科目を配置する分野 |
| ③情報学 | プログラミング言語を一種類以上学修できる科目を配置する分野 |
| ④データ サイエンス |
ITを利用してデータ解析を学修できる科目を配置する分野 |
| ⑤その他 （学科特有のデータを扱う授業） |
学科特有の「データの扱い方を学修できる」科目を配置する分野 |
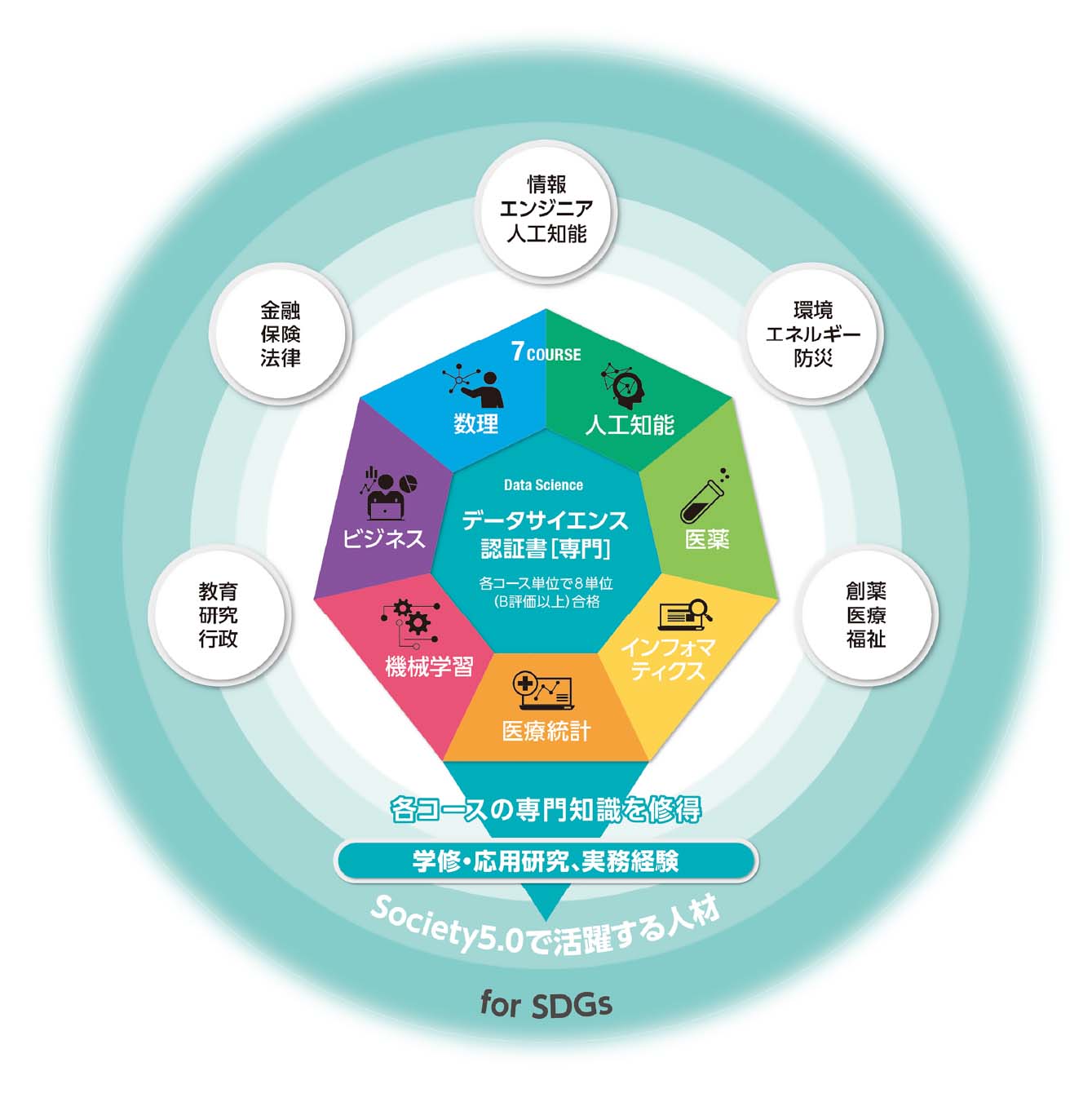
データサイエンスに関する専門的な知識・技術を学修することができる教育プログラムです。本プログラムは各キャンパスの特色を活かしたコース制としており、コースに配置されている科目の単位取得により、修了要件を満たした場合には、本学オリジナルの「データサイエンス認証書[専門](Data Science Certificate [Applied])」を授与します。
コースごとに設定する科目からで８単位(実データを扱う科目(１科目以上)の単位取得必須)をB評価以上の成績で合格すること。
| 神楽坂キャンパス | 数理コース、ビジネスコース |
|---|---|
| 野田キャンパス | 人工知能コース、医薬コース |
| 葛飾キャンパス | 機械学習コース、医療統計コース、Informatics コース |
応用数学と聞いて、どんな学問なのか、またどんなところで役立っているのか、なかなかイメージが湧きにくいかもしれませんが、実は私たちの身近なところや、社会の様々なところで力を発揮している学問なのです。本学科の教員が応用数学の魅力について紹介しますので、応用数学を身近に感じるとともに、その面白さも知ってください。
たくさんのデータの中から、似ているもののグループを見つけたいことがあります。例えば動画のサブスクリプションサービスの会社は、どの人がどの動画を見たかを記録したぼう大なデータを持っています。そこから「恋愛ドラマが好きな人」や「ファンタジー系のアニメが好きな人」のようなグループが見つけられれば、たくさんの新作動画の中からユーザの好きそうなものを「次はこれを観ませんか」とおすすめする、といったことが可能になります。このコラムではそのような方法のひとつであるK-平均法を紹介します。
詳しくはこちら（pdfファイル）