
応用数学科には次の3つの学びの分野があります。
どの分野でも、紙と鉛筆とコンピュータを駆使して問題に挑みます。

私たちの身の回りにはたくさんの「データ」が存在しますが、データをただ眺めているだけでは,何かに役立てることは出来ません。しかし、そこに統計学を用いることで、データの傾向を把握したり、将来の予測に役立てることができるのです。数理データサイエンス分野は、データを分析するだけでなく、データ分析手法の理論や方法論について、数学の知識を背景に学習・研究します。当学科では、基盤となる数学・数理統計学・プログラミングから始めて、この分野をしっかりと学習できるよう科目を設置しており、統計学の理論と応用の両方を学ぶことで、世の中の複雑な現象を予測・解明することができるようになります。
自然や社会に現れるさまざまな現象や問題を、数式に置き換えて表すことを数理モデリングと呼びます。本分野は、数理モデリングを通して現象の本質を理解し、さらに予測や最適化を行う学問分野です。複雑な現象を数式で表現し、計算処理することができれば、コンピュータの中だけでさまざまな状況を試すことができますが、そのためには基礎的な数学に加え、アルゴリズム(問題を効率的に解く方法論)や情報を扱う理論(情報理論)といった応用数学、さらに数理モデルをコンピュータ上で効率良く、正確にシミュレーションするための知識も必要です。当学科では、数理モデリングの基盤となる数学からコンピュータを用いた実践まで総合的に学習することができます。

コンピュータに人間のような、さらには人間を超えた知的な処理を行わせるための理論と実践を探求する学問分野です。人間とコンピュータでは得意なやり方が違うため、人間を単純にまねるのではなく、コンピュータ向きの処理方法を研究する必要があります。飛行機を作るときにそっくりそのまま鳥をまねるのではないのと同じです。当学科では、基盤となる数学やコンピュータサイエンスから始めて、処理対象である数式・図形や自然言語などをコンピュータでどのように扱うかまで、この分野をしっかりと学習できるよう科目を設置しています。

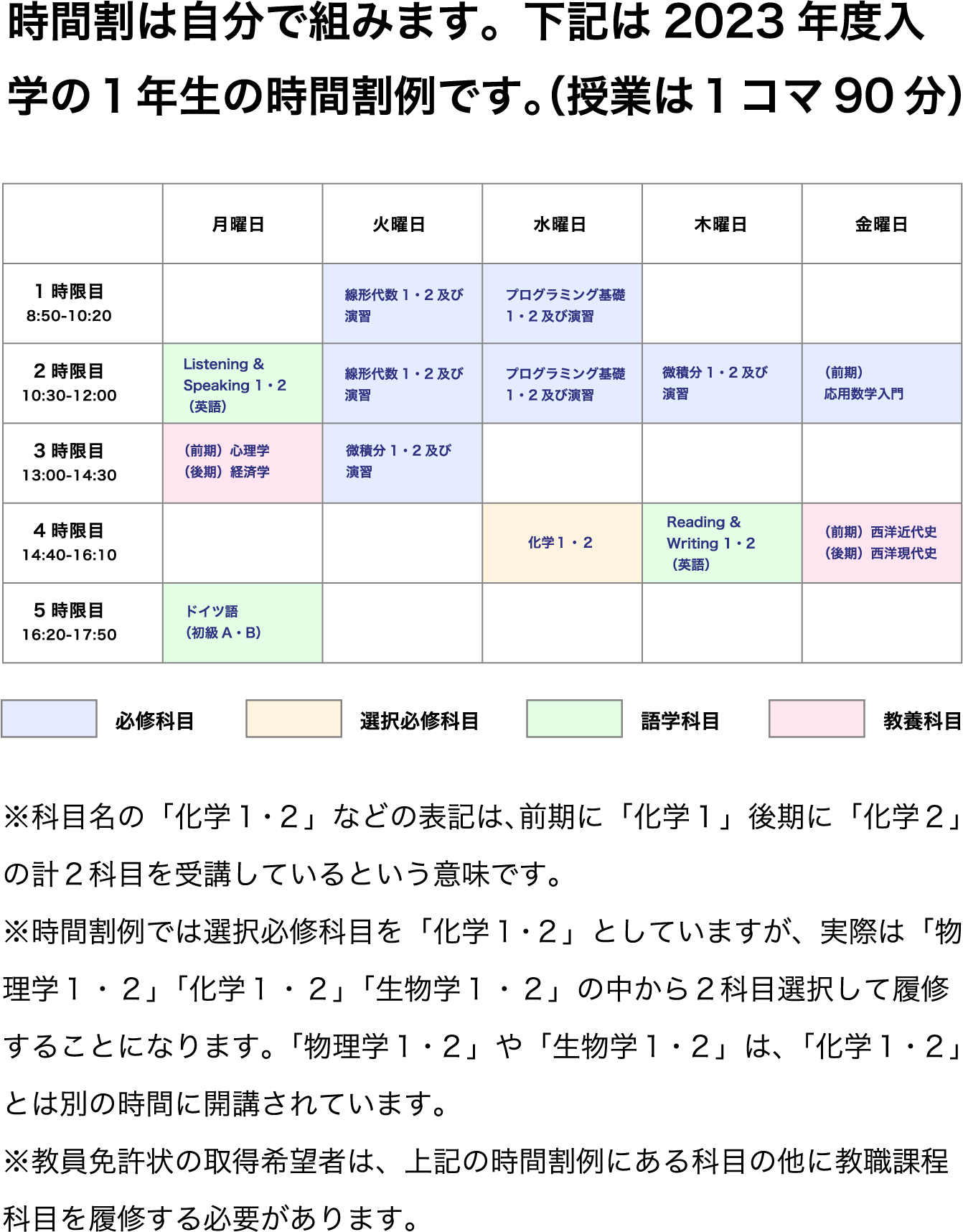
応用数学科のカリキュラムでは、1年次に応用数学のすべての分野(数理データサイエンス・数理モデリング・知能数理)の基礎となる数学やプログラミングの科目を学び、2年次には各分野の基礎科目を学びます。3・4年次には、1・2年次で学んだ基礎をもとに、より専門的な内容が学べるようになっています。
応用数学科のカリキュラムについてはこちらをご覧ください。
応用数学科や応用数学専攻(大学院)の卒業生は、様々な分野の第一線で活躍しています。
学部卒業生、大学院修了生の就職先や進学先などについて、詳しくはこちらをご覧ください。
過去のオープンキャンパスの様子や年間行事について、またフォトギャラリーを通じて応用数学科の授業風景や学生生活、イベントなどの様子をご紹介します。文字だけでは伝わらない応用数学科の雰囲気を知ってください。